Topic 4- Dynamics

Dynamics is the study of motion of an object with respect to forces that produce the motion. 

Force is defined as the one that changes body’s state of rest or of uniform motion in straight line. Another definition of force is that it causes a body to accelerate. The unit of force is newton (N). 1 newton is the force required to give a mass of 1 kg an acceleration of 1 ms-2.

Newton’s laws of motion

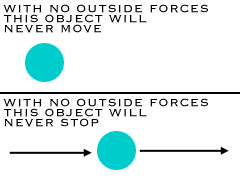
First Law

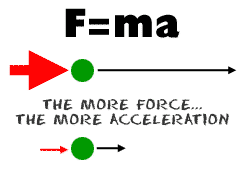
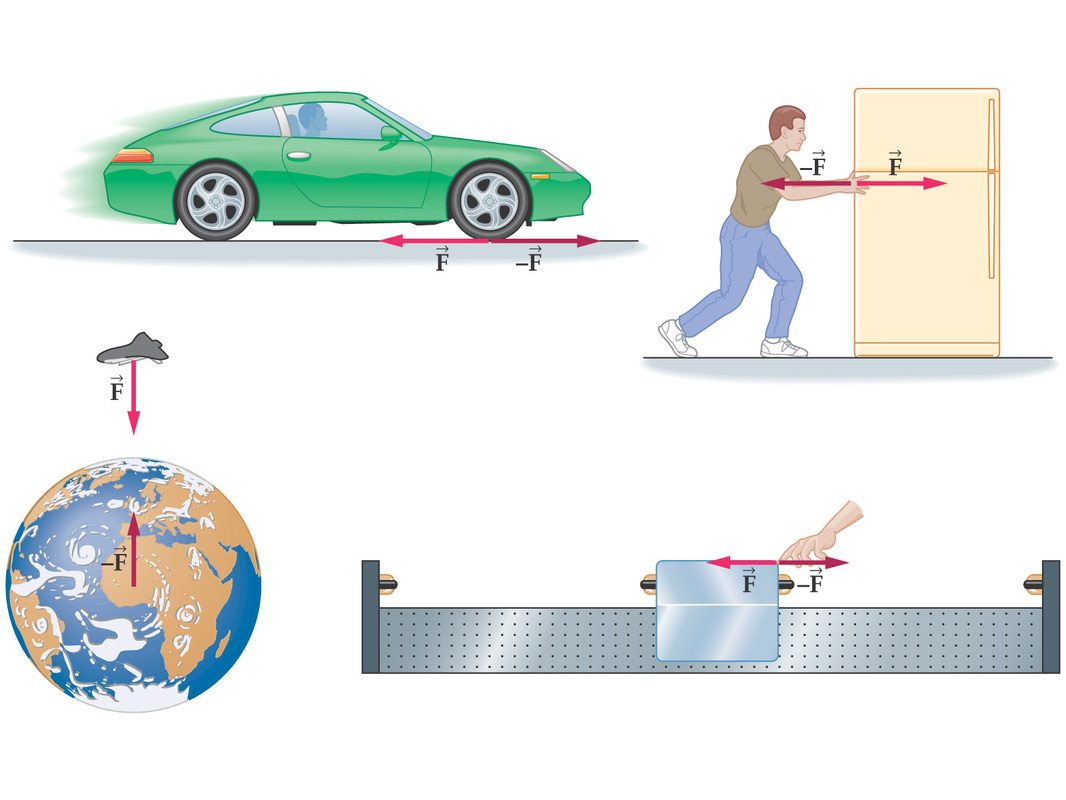
The first law says that an object at rest tends to stay at rest, and an object in motion tends to stay in motion, with the same direction and speed.

Second Law
The relationship between an object's mass m, its acceleration a, and the applied force F is F = ma. Acceleration and force are vectors (as indicated by their symbols being displayed in slant bold font); in this law the direction of the force vector is the same as the direction of the acceleration vector.

Third Law
The third law says that for every action (force) there is an equal and opposite reaction (force). Forces are found in pairs. Think about the time you sit in a chair. Your body exerts a force downward and that chair needs to exert an equal force upward or the chair will collapse. It's an issue of symmetry.

 

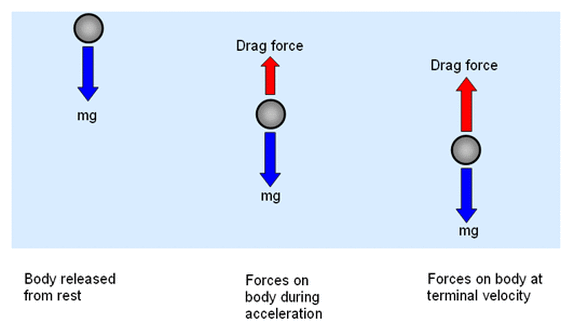
Acceleration due to gravity

Study the motion of a falling object.

This motion could be affected by:

• the mass of the object
• the height from which the object falls.

Carry out experiments to find out if these variables affect the motion of the falling object.

Find the acceleration due to gravity.

Useful equation: s=u·t+½·a·t2

As the velocity of the sphere increases so does the viscous force (air resistance) R, and eventually R becomes equal to W the weight. Since there is now no net force acting on it, its velocity has a constant maximum value known as terminal velocity. 

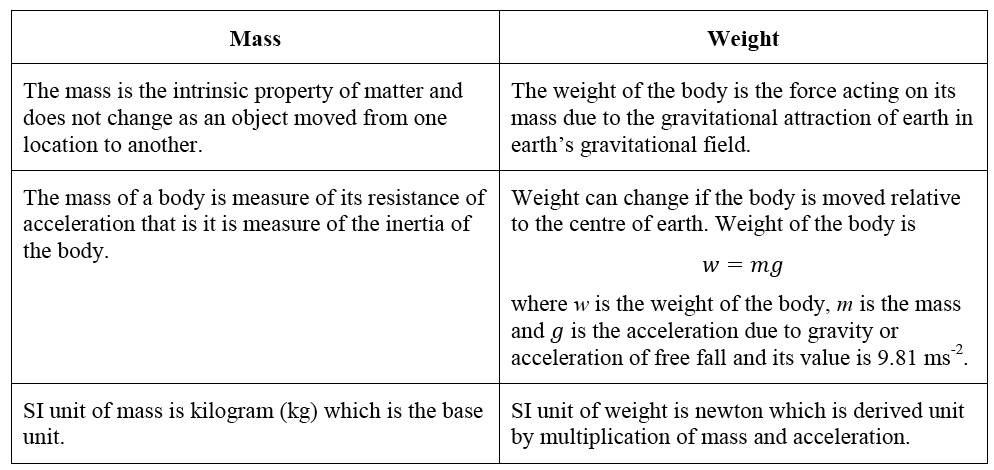
Mass & Weight

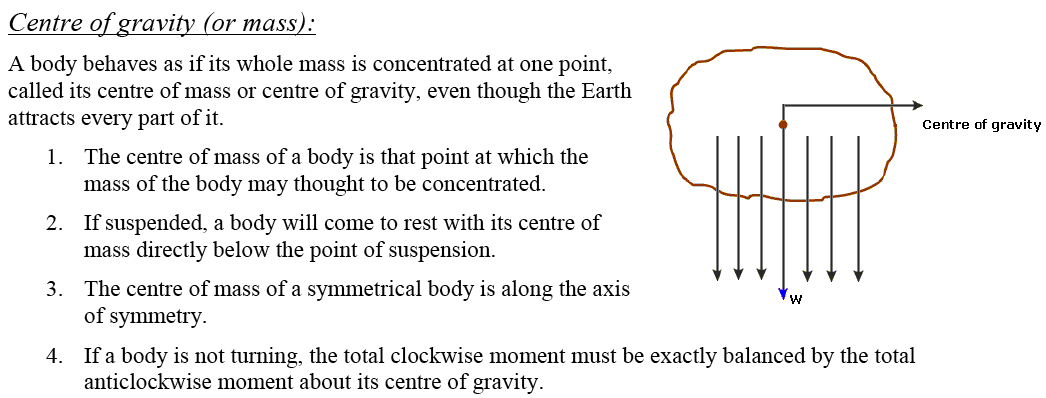
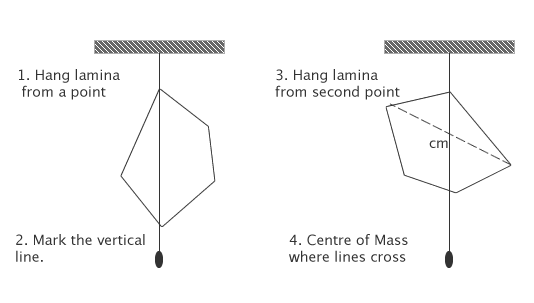
Centre of gravity (mass)

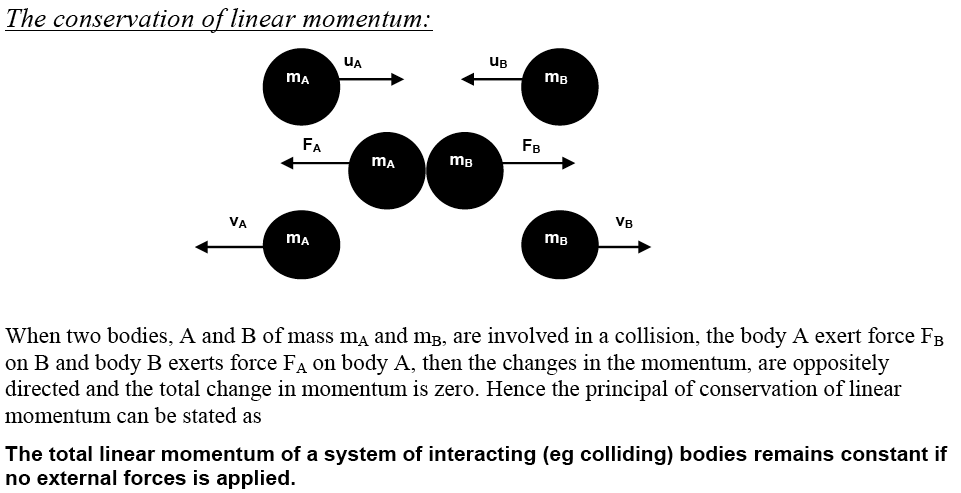
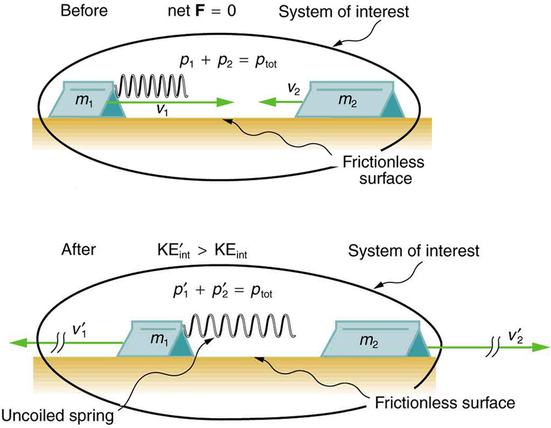
Linear momentum

Conservation of linear momentum

Newton's Cradle- is a clever device that uses a series of equal pendulums in a row to demonstrate the Laws of Conservation of Momentum and Conservation of Energy.

Practical Investigation- Loosing your marbles

Elastic and inelastic collisions

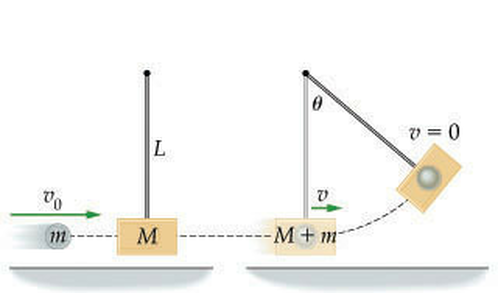
Ballistic pendulum

A 0.05 bullet with velocity 150 m/s is shot into a 3 kg ballistic pendulum. Find how high the pendulum rises after the bullet gets stuck inside.

First use conservation of momentum to find the final velocity of the bullet/pendulum.

This is an inelastic collision.

m1u1 + m2u2 = (m1+ m2)v

(0.05kg)(150m/s)+(3kg)(0m/s) = (3.05kg)v

v= 2.5 m/s

Now that we know the ballistic pendulum with the bullet in it begins to swing with a speed of 2.5 m/s, we use conservation of energy to find how high it swings.

0.5mv2^2= mgh

0.5m(2.5m/s)^2 = mgh

h= 0.32 m

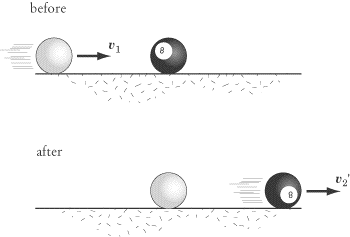
Billiards example

A billiards player hits the eight ball (0.15 kg mass), which is initially at rest, head-on with the cue ball (0.260 kg). The player strikes the cue ball with a velocity of 0.2 m/s causing the eight ball to speed away at 0.1 m/s. What is the velocities of the cue ball after the collision? Assume the collision is perfectly elastic,

m1u1 + m2u2 = m1v1 + m2v2 

Solve this problem in your notebooks.

Collision simulation lab

A special case of Newton's second law of motion

Notice that impulse is measured in N-s (pronounced "Newton seconds") and that change in momentum is measured in kg-m/s (pronounced "kilogram meter per second"). 

Since the above derivation shows that an impulse is equal to a change in momentum, these two units must be equivalent, and they are.

Using your understanding of base SI units prove that these units are equivalent.