Topic 5- Forces
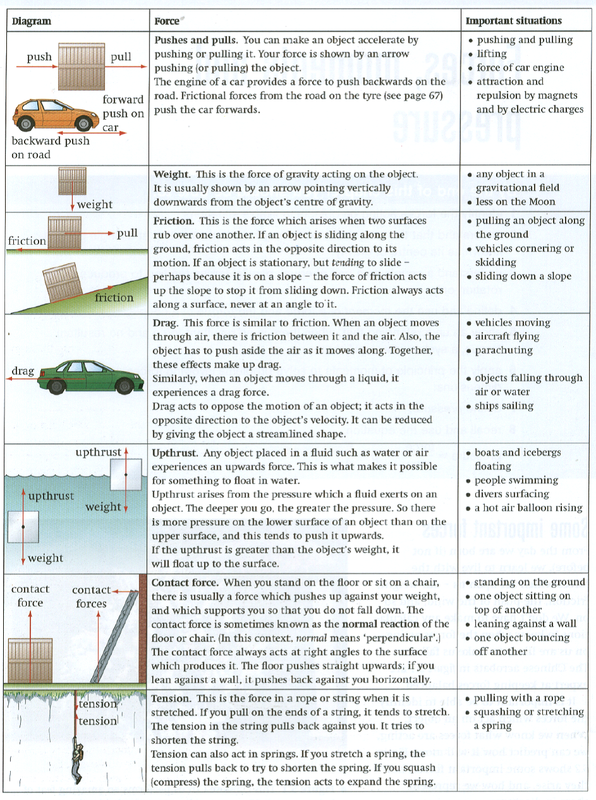
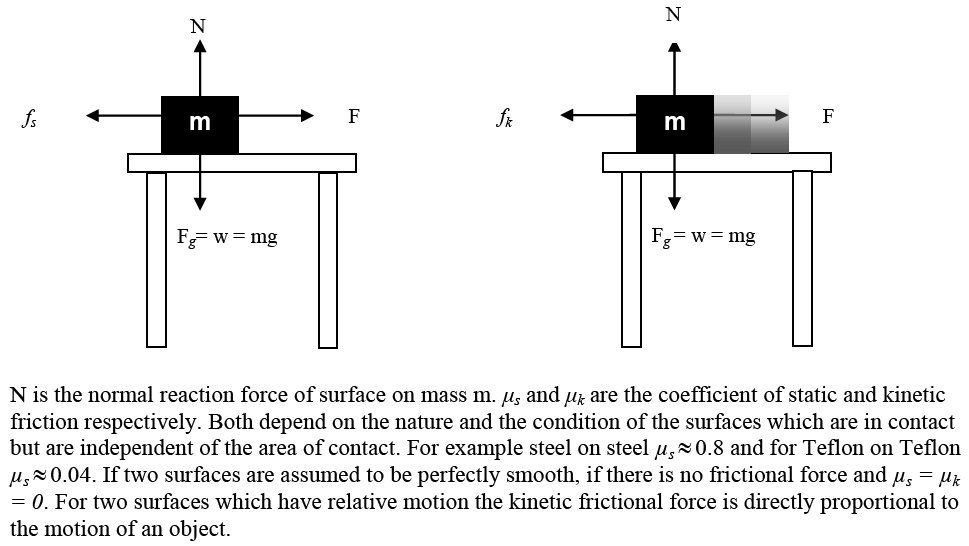
Force is defined as the one that changes body’s state of rest or of uniform motion in straight line. Another definition of force is that it causes a body to accelerate. The unit of force is newton (N). 1 newton is the force required to give a mass of 1 kg an acceleration of 1 ms-2.
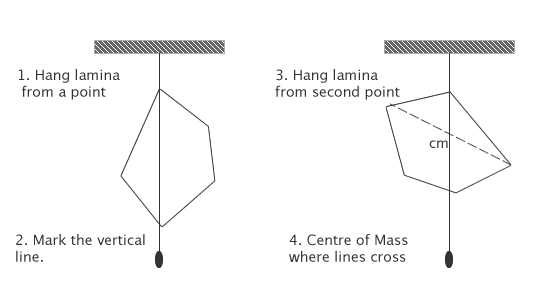
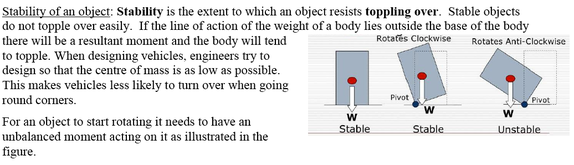
Centre of gravity (mass)
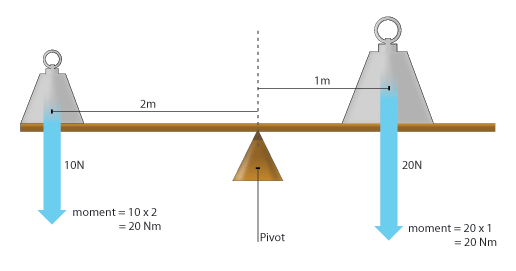
Moments of force
Linear momentum
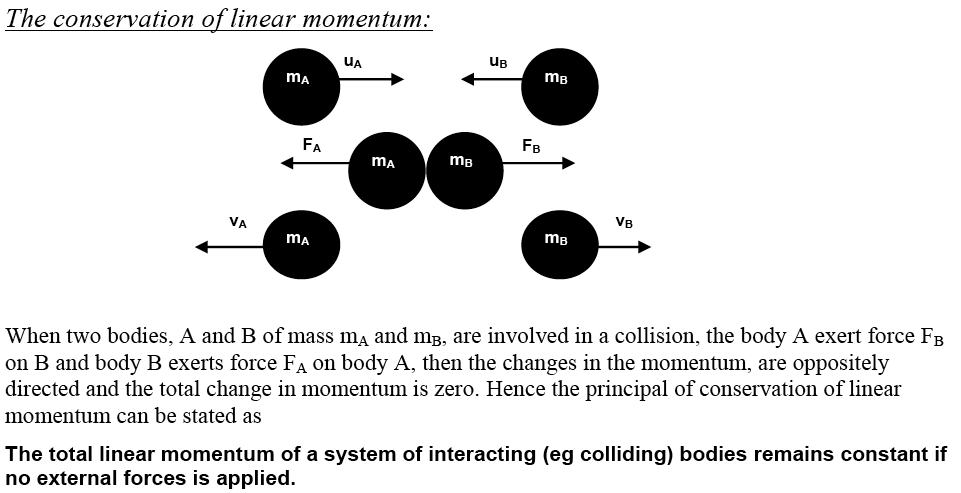
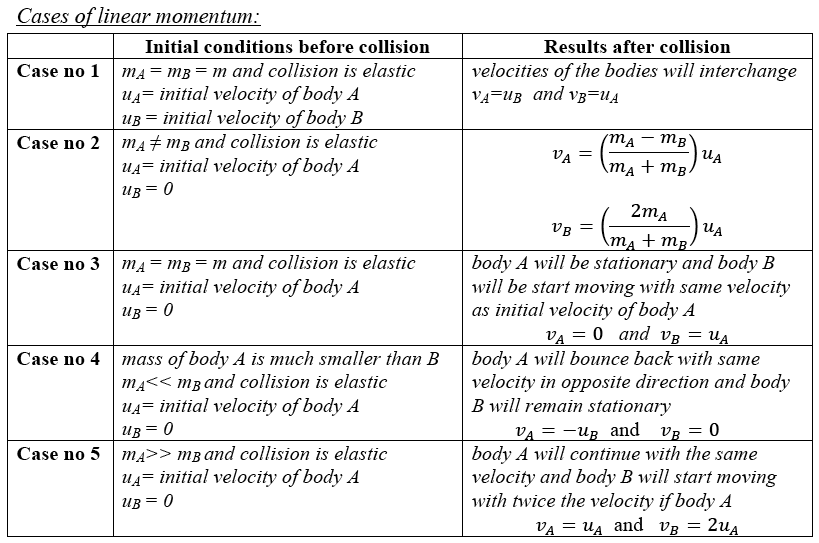
Conservation of linear momentum
Elastic and inelastic collisions
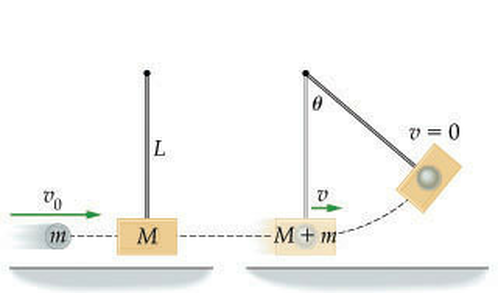
Ballistic pendulum
A 0.05 bullet with velocity 150 m/s is shot into a 3 kg ballistic pendulum. Find how high the pendulum rises after the bullet gets stuck inside.
First use conservation of momentum to find the final velocity of the bullet/pendulum.
This is an inelastic collision.
m1u1 + m2u2 = (m1+ m2)v
(0.05kg)(150m/s)+(3kg)(0m/s) = (3.05kg)v
v= 2.5 m/s
Now that we know the ballistic pendulum with the bullet in it begins to swing with a speed of 2.5 m/s, we use conservation of energy to find how high it swings.
0.5mv2^2= mgh
0.5m(2.5m/s)^2 = mgh
h= 0.32 m
First use conservation of momentum to find the final velocity of the bullet/pendulum.
This is an inelastic collision.
m1u1 + m2u2 = (m1+ m2)v
(0.05kg)(150m/s)+(3kg)(0m/s) = (3.05kg)v
v= 2.5 m/s
Now that we know the ballistic pendulum with the bullet in it begins to swing with a speed of 2.5 m/s, we use conservation of energy to find how high it swings.
0.5mv2^2= mgh
0.5m(2.5m/s)^2 = mgh
h= 0.32 m
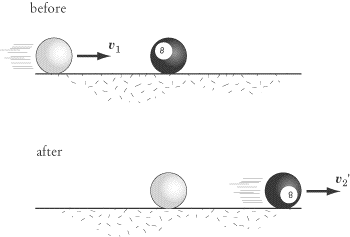
Billiards example
A billiards player hits the eight ball (0.15 kg mass), which is initially at rest, head-on with the cue ball (0.260 kg). The player strikes the cue ball with a velocity of 0.2 m/s causing the eight ball to speed away at 0.1 m/s. What is the velocities of the cue ball after the collision? Assume the collision is perfectly elastic,
m1u1 + m2u2 = m1v1 + m2v2
Solve this problem in your notebooks.
m1u1 + m2u2 = m1v1 + m2v2
Solve this problem in your notebooks.
Collision simulation lab
A special case of Newton's second law of motion
Notice that impulse is measured in N-s (pronounced "Newton seconds") and that change in momentum is measured in kg-m/s (pronounced "kilogram meter per second").
Since the above derivation shows that an impulse is equal to a change in momentum, these two units must be equivalent, and they are.
Using your understanding of base SI units prove that these units are equivalent.
Since the above derivation shows that an impulse is equal to a change in momentum, these two units must be equivalent, and they are.
Using your understanding of base SI units prove that these units are equivalent.